Human centered CACC design
a comfortable longitudinal vehicle controller
Motivation
With the development of autonomous driving systems, the role of the human has been transited from driver to passenger/supervisor. In this project, a novel autonomous longitudinal vehicle controller is designed to improve human comfort.
Methodologies
- The jerk (derivatives of longituinal acceleration) is used to quantify the physical comfort of the driver and driving smoothness.
- The psychophysical car-following model (i.e., AP model) is used to quantify psychological comfort of the driver. As shown in the following figure, different driving regimes in the psychophysical car-following model are separated based on the human driver’s perceptual thresholds. For example, BX represents the minimum following threshold for the human driver. Here, we focus more on the unconscious regime (white area), where a human driver cannot perceive any relative motion with the preceding car despite unconsciously generating small acceleration/deceleration. Suppose we can design a controller such that the vehicle motion states are within the unconscious regime. In that case, the human’s nerve is less stimulated during the normal operating mode and more relaxed.
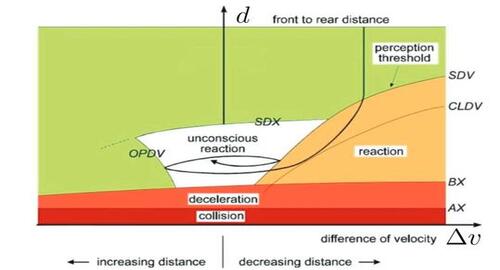
In this way, the human workload in monitoring the CACC car operation can also be reduced since the human nerve is less stimulated during the normal operating mode.
- An MPC-like optimal controller is designed to improve both physicaland psychological comfort. The optimal control problem is formulated as follows:
\(\qquad J_i=c_1 \sum^{T_b} \| d_i \|_2 + c_2 \sum^{T_b}\|u_i\|_2 + c_3 \sum^{T_b} \|jerk_i \|_2 + c_4 \sum^{T_b} \| z_i \|.
\label{cost_function}\)
\(\qquad\) with constraints:
\(\begin{aligned}
\qquad\qquad &\|\lambda_i(t)-\lambda_{i}(0)\|_p \leq \|\lambda_{i-1}(t)-\lambda_{i-1}(0)\|_p\\
&\|\lambda_{i+j}(t)-\lambda_{i+j}(0)\|_2 \leq \|G^*_{h_a}(s)\|_\infty\|\lambda_1(t)-\lambda_1(0)\|_2\\
&\|\lambda_{i+j}(t)-\lambda_{i+j}(0)\|_\infty \leq \|g^*_{h_a}(t)\|_1\|\lambda_1(t)-\lambda_{1}(0)\|_\infty\\
&d_{i+j}(t)\geq \max\{TTC\left(v_{i+j}(t)-v_{i+j-1}(t)\right),d_{\min}\}
\end{aligned}\)
\(\qquad\)The details can be found in our paper [1].
Results
- The simulation has been done with MATLAB+SIMULINK+CARSIM. Animation is shown in the following video.
- Comparing to the benchmark controller design, the human driver comfort have been improved largely.
- The codes can be found in my Github repository
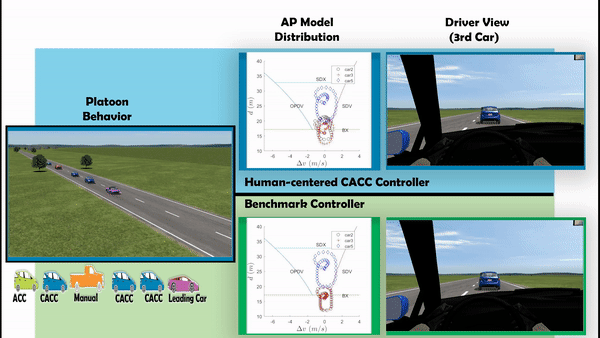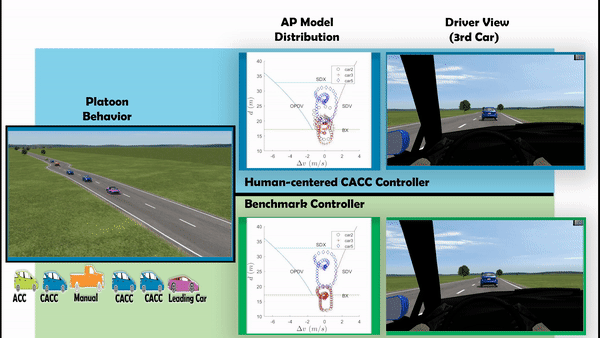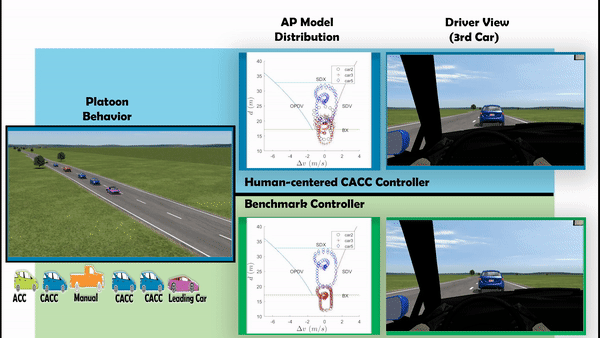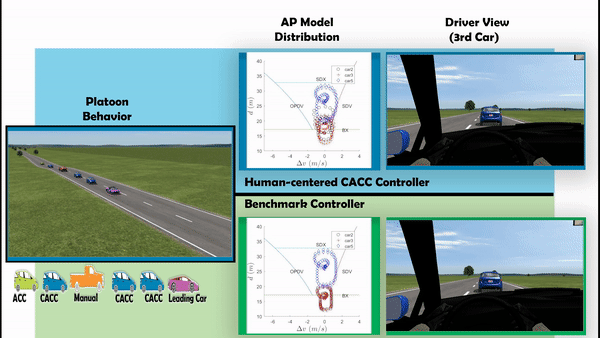
Application
- An autonomous vehicle longitudinal controller is designed to improve driver comfort.
- This controller can also help human performance in monitoring the operation of the autonomous driving system (longitudinal).